Upwords: Better Laid Plans
Getting excited about a trivial problem
If you’ve ever played Scrabble or Words with Friends, you’ll be familiar with tile-based word games. I play a similar game called Upwords, where the twist is that you’re also allowed to stack tiles on top of existing ones. I’ll let Wikipedia introduce it:
Upwords is a letter tile word game similar to Scrabble, with players building words using letter tiles on a gridded game board. Unlike Scrabble, in Upwords letters can be stacked on top of existing words to create new words. Scoring is determined by the number of letter tiles stacked in a new word.
There’s an iOS and Android app for it where you can play against friends or strangers, and there are leaderboards for three categories: Highest Rank (basically just an ELO rating), Highest Score (most points scored in a game), and Best Single Play. When I was looking at this third category, the rankings stood out:
Best_Laid_Plans in first place jumps out for being so far ahead of the pack. I assumed that they must have deliberately constructed this, as it didn’t make sense otherwise for there to be such a large gap.
The idea of trying to deliberately construct a play to get into the leaderboard is just the kind of trivial problem that scratches a certain itch for me. It turned into a project spanning over a year where I learned a whole lot about software testing, algorithms, and data structures. I’d like to share that journey with you.
What’s possible?
First, let’s see an example of how scoring works. Instead of receiving points based on the rarity of the letter, each tile is worth 1 point, and you get points based on how high a square has been stacked. For example, in this board:

if you played the word “LAYER” across like so (while newly forming “LAY and “GIVER” vertically):
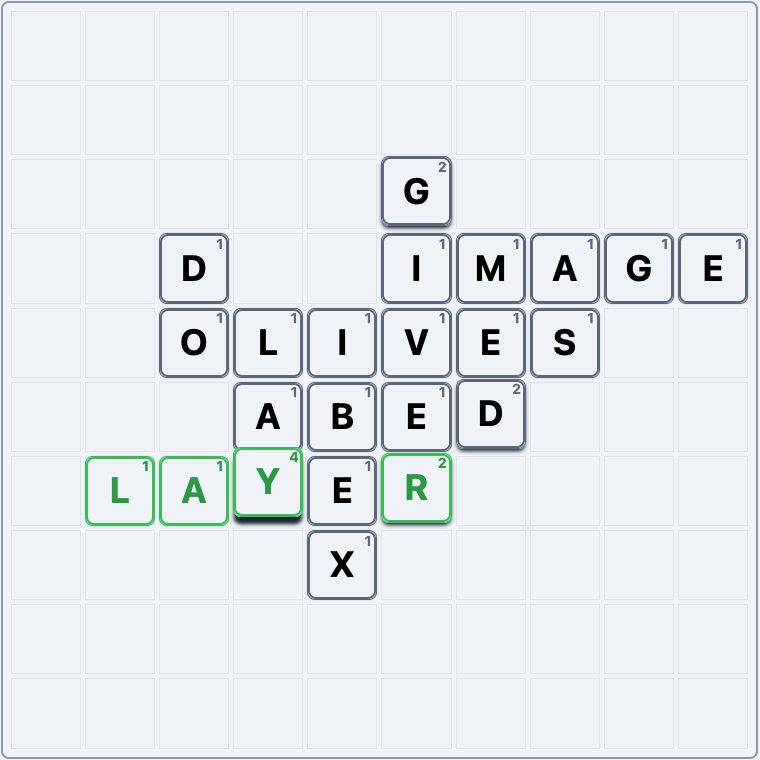
you would get 22 points: 9 points for “LAYER”, 6 for “LAY”, and 7 for “GIVER”. As this example shows, the tiles on the intersections get double-counted.
A tile can’t be stacked higher than 5, so in normal play there’s a certain strategy to trying to get the play which puts the 5th tile and denying the same to your opponent(s). To figure out how to get to the top spot on the leaderboard, let’s work backwards: we’ll think about what the best possible score for a play is, and that should give us a pretty good idea of how to get something that’s “good enough”.
What do we know?
- The more tiles on the board, the higher the score can be. The game finishes as soon as someone uses up their tiles, so with a 2-player game the other player needs to have at least 1 tile left in their rack.
- There’s a 20 point bonus for playing all 7 of your tiles. This seems that it should obviously be used.
- Together with point 1, we can calculate based on the standard set of 100 tiles that there should be 92 tiles played on the board, 7 in your rack, 1 in your opponent’s, and your play should use all 7 tiles.
- A tile is counted once per each newly formed word that it’s part of. Any tile that’s scored can either be part of 1 or 2 words; the ones that are at the intersection of two formed words will be counted twice. Because words are only formed adjacently to tiles placed down, this means a maximum of 7 squares which will be “double-counted”.
- A corollary of this is that, if a tile isn’t double-counted, as long as it’s in line with a formed word it doesn’t matter how high it is. A 3-1-4-2-4-4 high word is counted the same as a 3-5-5-5 word (both have 18 tiles). This play:

 scores the exact same as this one:
scores the exact same as this one:


- It follows that we can ignore the specific placement of most tiles, as long as they are included in the formed words.
- A corollary of this is that, if a tile isn’t double-counted, as long as it’s in line with a formed word it doesn’t matter how high it is. A 3-1-4-2-4-4 high word is counted the same as a 3-5-5-5 word (both have 18 tiles). This play:
Given these points, we know that
- 92 tiles are on the board, 7 will be played
- The 7 tiles played will be double counted, so we want to maximize them: they should be played onto 4-tile high “word intersections”. This means that 28 tiles (of the 92 on the board) will be stacked to 4 on the “intersections”.
- All remaining tiles simply need to be in line with either the big 7-letter word, or one of the “offshoots”.
By arranging the tiles like this, we will maximize the double-counted tiles, and ensure that all tiles on the board will be counted towards the final score.

With 100 available tiles, we can calculate what the total score would be:
<double counted tiles> * 2 + <single counted tiles> + <7-tile bonus>
= 35 * 2 + (92-28) + 20
= 70 + 64 + 20
= 154
154 points is what the top of the leaderboard already had. Their username Best_Laid_Plans made sense now; I’d been beaten to the punch before I even started. They must have figured out the exact same thing, constructed a perfect configuration, and managed to play a word that maximized their point total.
Squeezing out Bonus Points
This was a rough start and I was ready to move on, until I realized that there are two extra bonus point rules that could be used to potentially score higher.
The first is for words formed with only one-high tiles. The tile score is doubled for such words.
The second is obscure and buried deep within the rules; I actually didn’t discover it until later. The rule is that, in conjunction with the single-tile-height bonus, if you play a “Qu” tile, it counts for 2 extra bonus points. The app doesn’t even include this in their FAQ and How to Play section, but it does score it correctly. I actually thought it was a bug until I looked up the official ruleset PDF of a physical copy, and sure enough there it was: https://winning-moves.com/images/UPWORDS_rulesv2.pdf
These two bonus point rules allow us to slightly improve on the straightforward 154 limit, but in turn it requires a more constrained board setup ahead of the final move.
Calculating the target
We’l focus on the first bonus point rule for now. Let’s take our previous configuration, where we had 7 tiles stacked to height 4 (5 after the final play), which are double counted. By “flattening” that word out, we will lose out on the double-counting effect, but in turn the vertically formed word receives bonus points for being only one high. Consider these two board states:

They each use the same number of tiles, but in the example on the left, playing “HOMESICK / SEATS” will pick up an extra 8 bonus points, because all the tiles are 1 tile high. This is somewhat offset by losing the double-counted 4-high tile, but overall it’s positive. (In the above example, “HOMESICK / SEATS” is 32 while “MINT / MEATS” is 28 points.)
The maximum length that a word can be is 10 tiles. If we “flatten” a tile that would have been 5-high, we will lose 4 points from the lost double counting, but every tile in the newly formed 1-high word will get 1 bonus point: -4 + 10 = +6. However, this comes with a problem. Previously, the secondary word that was formed was already on the board and connected to the main word. But now, we want to place a single-tile high word (remember, for the bonus points all letters in a word must be one-tile high), so the space needs to be empty. Similar to Scrabble, the game rules don’t allow for unconnected placements. This means that we need to use extra “connection” tiles to have the one-high word in place.
In our example above, the connecting tiles R and F in “REF” aren’t included in the final word. Granted, we’re gaining a maximum of 6 points on the previous setup so we could spare a few tiles and still beat the record. But we don’t have to; here’s a configuration that keeps those tiles connected, and have the connecting tiles be part of the final score:
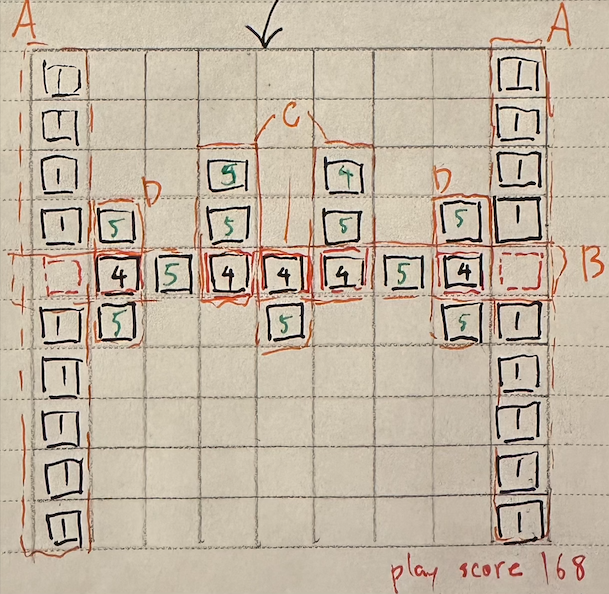
Oh boy, that’s very messy. In the next post, I’ll go in-depth on this configuration, what each of the annotations mean, and how it gets us to a possible score of 168.
